本文共 8191 字,大约阅读时间需要 27 分钟。
该篇涉及内容比较多就不多于废话了,直接x入主题
PathMotion
抽象类PathMotion一个与路径移动相关的,这个基类可以扩展提供运动沿着路径转换,比如指定两个位置进行移动,通过PathMotion路径下指定维度进行移动。该类提供了一个getPath方法,源码如下
public abstract class PathMotion { public PathMotion() {} public PathMotion(Context context, AttributeSet attrs) {} /** * Provide a Path to interpolate between two points (startX, startY) and * (endX, endY). This allows controlled curved motion along two dimensions. * * @param startX The x coordinate of the starting point. * @param startY The y coordinate of the starting point. * @param endX The x coordinate of the ending point. * @param endY The y coordinate of the ending point. * @return A Path along which the points should be interpolated. The returned Path * must start at point (startX, startY), typically using * {@link android.graphics.Path#moveTo(float, float)} and end at (endX, endY). */ public abstract Path getPath(float startX, float startY, float endX, float endY);} 在Transition里面有具体实现,默认的是直线路径
private static final PathMotion STRAIGHT_PATH_MOTION = new PathMotion() { @Override public Path getPath(float startX, float startY, float endX, float endY) { Path path = new Path(); path.moveTo(startX, startY); path.lineTo(endX, endY); return path; } }; 然而这种效果并不是很友好的,它的继承类Arcmotion诞生了,该类提供了自定义属性:minimumVerticalAngle、minimumHorizontalAngle、ArcMotion_maximumAngle水平方向和垂直方向的最小最大维度。以便于我们xml自定义ChangeBounds引用,getPath经过算法处理得到最终的路径。ChangeBounds本质是一个继承自Transition的类,如果引用了我们自定义的ArcMotion就替换了Transtion默认的直线路径移动,ChangeBounds稍后再细说,先来看看我们该怎么在xml引用自定义的ArcMotion
AutoTransition
工具类,当我们执行ChangeBounds相同控件Id位移渐变,而多余的控件要进行fade变化,该类帮助我们进行移动和调整大小视图中一个场景的变化。
public class AutoTransition extends TransitionSet { /** * Constructs an AutoTransition object, which is a TransitionSet which * first fades out disappearing targets, then moves and resizes existing * targets, and finally fades in appearing targets. * */ public AutoTransition() { init(); } public AutoTransition(Context context, AttributeSet attrs) { super(context, attrs); init(); } private void init() { setOrdering(ORDERING_SEQUENTIAL); addTransition(new Fade(Fade.OUT)). addTransition(new ChangeBounds()). addTransition(new Fade(Fade.IN)); }} 这里的Fade是Transition的子类Visibility的子类,自定义属性提供了Fade的mode设置fadingMode,Fade.in Fade.out值来自其父类的transitionVisibilityMode属性对应的mode,从源码里面不难看出这是一个简单的透明度变化的属性动画
private Animator createAnimation(final View view, float startAlpha, final float endAlpha) { if (startAlpha == endAlpha) { return null; } view.setTransitionAlpha(startAlpha); final ObjectAnimator anim = ObjectAnimator.ofFloat(view, "transitionAlpha", endAlpha); if (DBG) { Log.d(LOG_TAG, "Created animator " + anim); } final FadeAnimatorListener listener = new FadeAnimatorListener(view); anim.addListener(listener); anim.addPauseListener(listener); addListener(new TransitionListenerAdapter() { @Override public void onTransitionEnd(Transition transition) { view.setTransitionAlpha(1); } }); return anim; } Change系列
ChangeBounds这一过渡捕捉目标视图的布局范围场景改变前后的变化。提供属性是否支持大小裁剪,默认不支持,该类通过Property封装了一系列的键值对,供createAnimator调用,类似ChangeBounds的类还有好几个就不一 一细说,下面列出来如果你感兴趣可以查看相关源码(Change系列与Scene配合TransitionManager使用下面Demo介绍):
ChangeBounds
ChangeClipBounds
ChangeImageTransfor
ChangeScroll
ChangeTransform
官方demo实践
BasicTransition
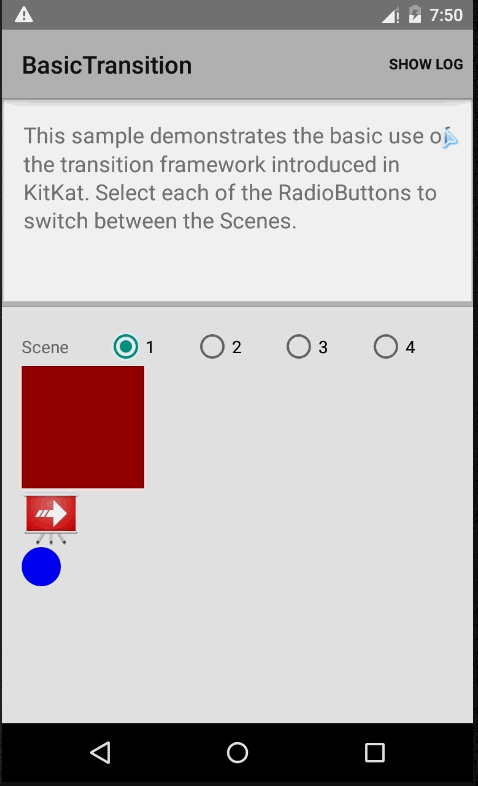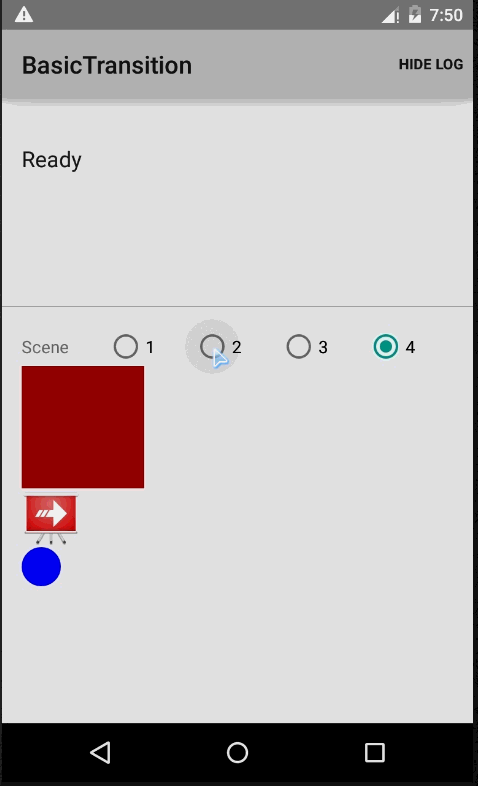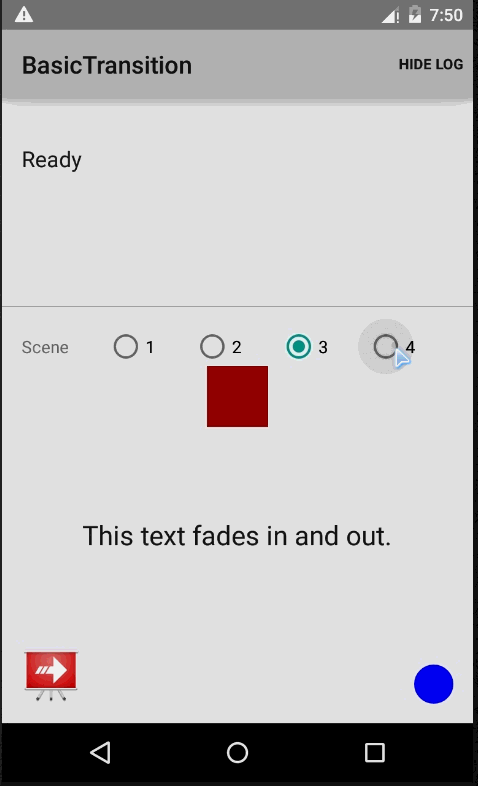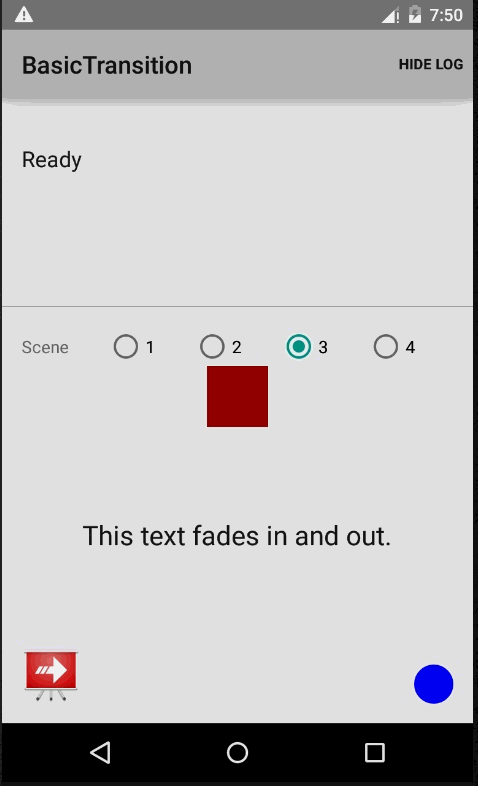
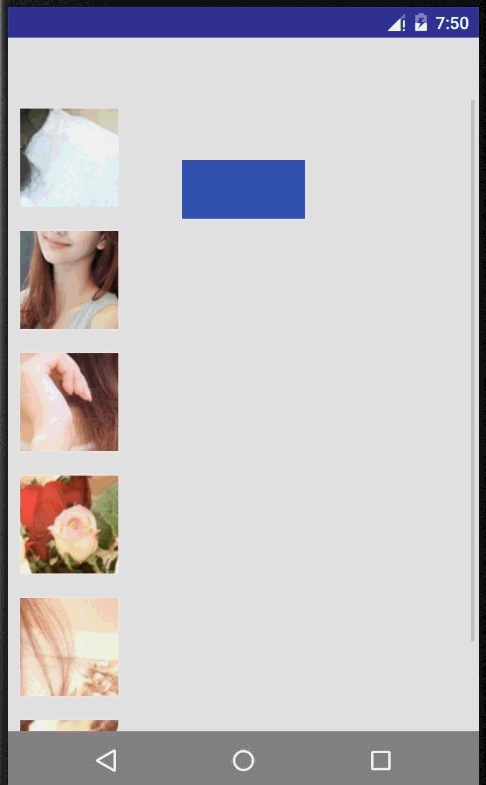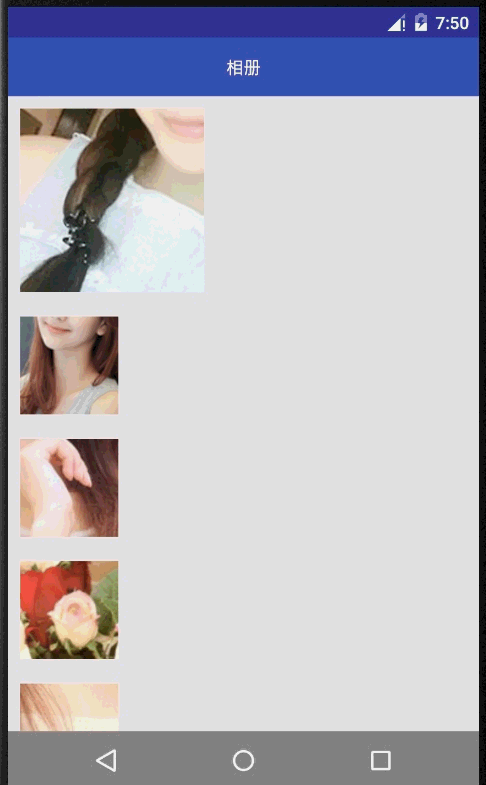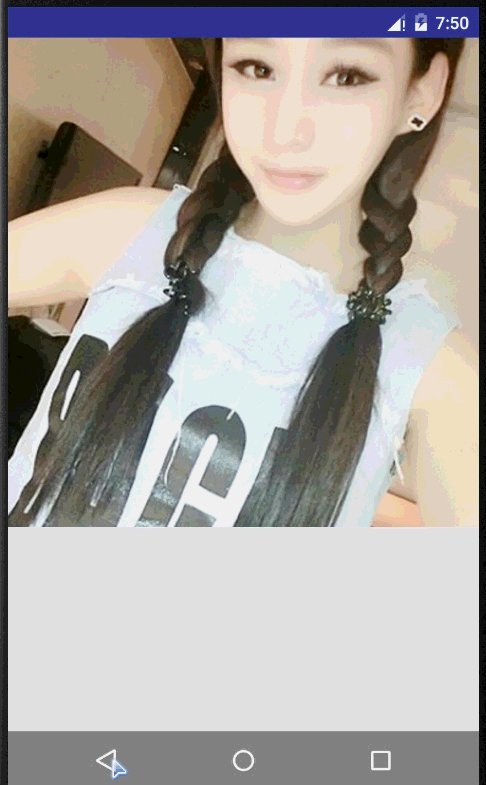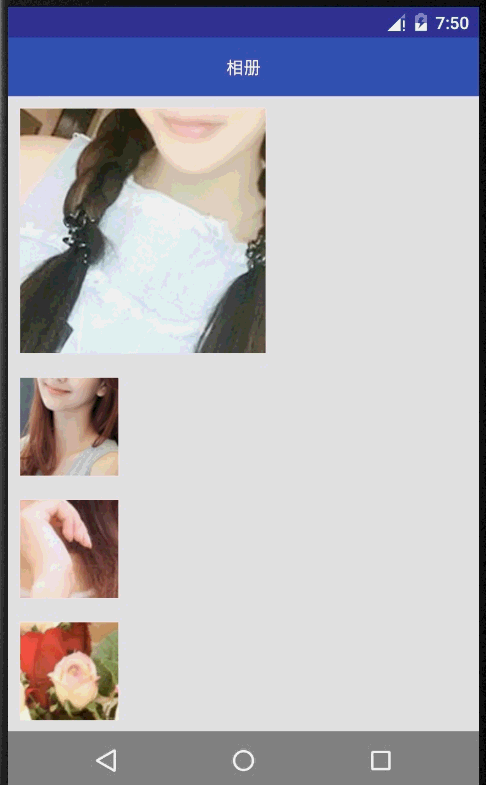
透过上面这一点源码粗略过一遍,在脑海中有了多多少少的一点印象,下面开始通过一些demo,来帮助我们进一步的了解Transition。官网提供了一个,实现效果如下:
实现原理:首先要有一个根布局rootView,其次是多个场景View,通过TransitionManager.go(Scene)进行场景变换(注意场景的view对应的id要相同才有效果),而Scene的实例获取方式可以通过new和getSceneForLayout方式,下面来简单看看demo核心代码示例:
public class BasicTransitionFragment extends Fragment implements RadioGroup.OnCheckedChangeListener { //.........略.............. @Override public View onCreateView(LayoutInflater inflater, ViewGroup container, Bundle savedInstanceState) { mSceneRoot = (ViewGroup) view.findViewById(R.id.scene_root); mScene1 = new Scene(mSceneRoot, (ViewGroup) mSceneRoot.findViewById(R.id.container)); mScene2 = Scene.getSceneForLayout(mSceneRoot, R.layout.scene2, getActivity()); mScene3 = Scene.getSceneForLayout(mSceneRoot, R.layout.scene3, getActivity()); mTransitionManagerForScene3 = TransitionInflater.from(getActivity()) .inflateTransitionManager(R.transition.scene3_transition_manager, mSceneRoot); return view; } @Override public void onCheckedChanged(RadioGroup group, int checkedId) { switch (checkedId) { case R.id.select_scene_1: { TransitionManager.go(mScene1); break; } case R.id.select_scene_2: { TransitionManager.go(mScene2); break; } case R.id.select_scene_3: { mTransitionManagerForScene3.transitionTo(mScene3); break; } case R.id.select_scene_4: { //缩放动画完成后重新设置控件大小 TransitionManager.beginDelayedTransition(mSceneRoot); View square = mSceneRoot.findViewById(R.id.transition_square); ViewGroup.LayoutParams params = square.getLayoutParams(); int newSize = getResources().getDimensionPixelSize(R.dimen.square_size_expanded); params.width = newSize; params.height = newSize; square.setLayoutParams(params); break; } } }} 场景的转换我们可以通过TransitionManager.go也可以通过上面代码中的TransitionInflater获取TransitionManager实例调用内部定义的其静态方法transitionTo。
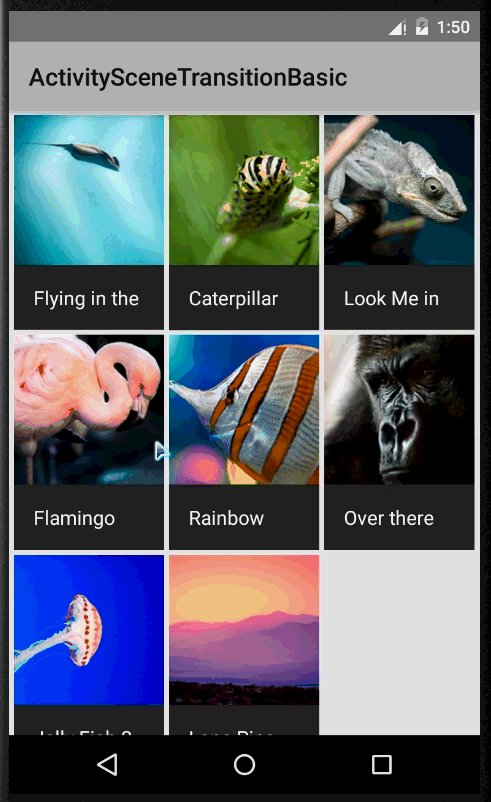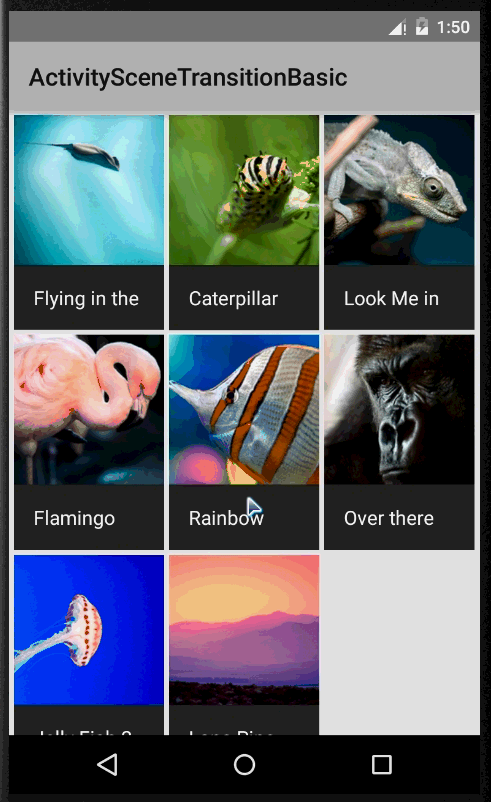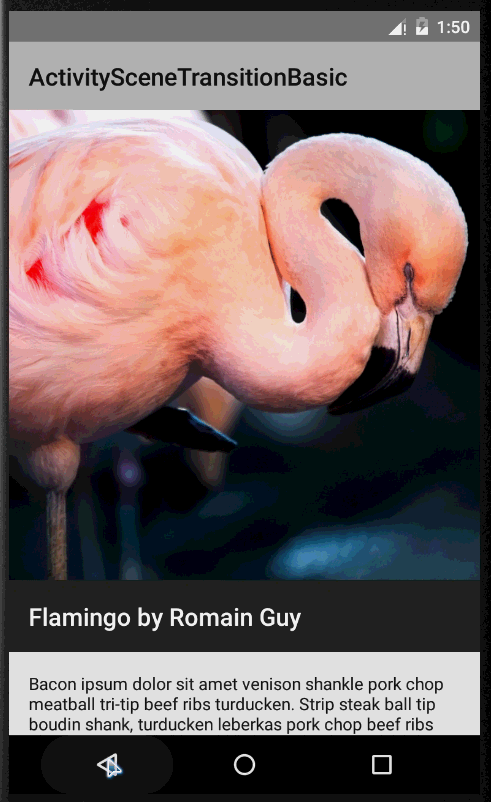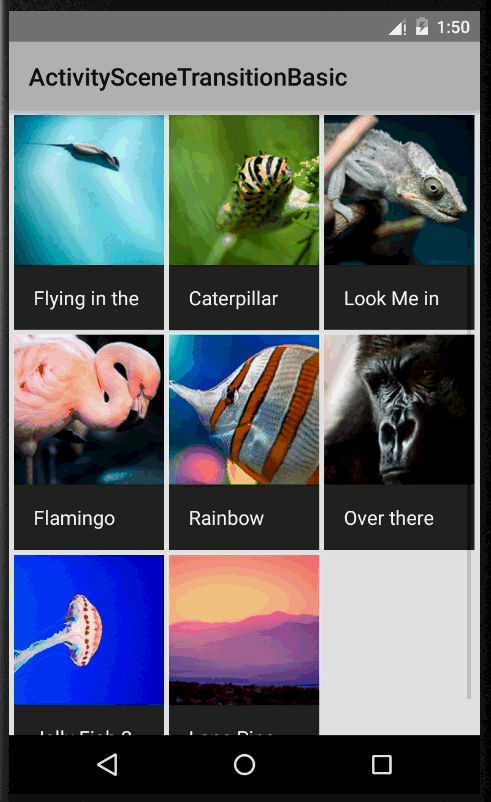
ActivitySceneTransitionBasic
这是一个官方提供的一个Activity无缝切换的demo,Activity的切换通过ActivityOptionsCompat向下兼容,调用ActivityOptionsCompat的startActivity方法,Pair形式封装的键要与跳转界面的值一致。官方源码跳转代码如下(这种效果比较适合用于列表跳转详情界面,起点小说的app就是如此实现)
@Override public void onItemClick(AdapterView adapterView, View view, int position, long id) { Item item = (Item) adapterView.getItemAtPosition(position); Intent intent = new Intent(this, DetailActivity.class); intent.putExtra(DetailActivity.EXTRA_PARAM_ID, item.getId()); ActivityOptionsCompat activityOptions = ActivityOptionsCompat.makeSceneTransitionAnimation( this, new Pair (view.findViewById(R.id.imageview_item), DetailActivity.VIEW_NAME_HEADER_IMAGE), new Pair (view.findViewById(R.id.textview_name), DetailActivity.VIEW_NAME_HEADER_TITLE)); ActivityCompat.startActivity(this, intent, activityOptions.toBundle()); }//...............下面是详情界面,接手传递数据调用transition方法................................ mItem = Item.getItem(getIntent().getIntExtra(EXTRA_PARAM_ID, 0)); mHeaderImageView = (ImageView) findViewById(R.id.imageview_header); mHeaderTitle = (TextView) findViewById(R.id.textview_title); ViewCompat.setTransitionName(mHeaderImageView, VIEW_NAME_HEADER_IMAGE); ViewCompat.setTransitionName(mHeaderTitle, VIEW_NAME_HEADER_TITLE); 当然如果需要变化的View只有一个就没必要用Pair了,直接调用makeSceneTransitionAnimation(Activity activity,View sharedElement, String sharedElementName) {}即可,实现效果图如下:
开源库Interpolator
动画都少不了插值器,Transition配合Interpolator让效果显得更PL了,在这里推荐两个比较不错的动画插值器相关的库,有了它们基本足以满足我们的开发需求
根据现在了解的Transition系列相关的只是,做一个简单的demo测试一下,效果图如下(录制效果不好见谅哈):
Transition相关的开发中,我们有必要明确一下几点区别:Enter、Exit、ReEnter、allow等相关属性含义,这里以下列代码为例做个简短说明
- true
- true
- true
- @transition/scene1
- @transition/scene1
- @transition/scene1
- @transition/scene1
- @transition/scene1
- @transition/scene1
当然这些属性我们可以不仅可以在Style中定义,还可以代码调用通过Window、Slide等进行配置,在动画执行的时候还可以添加监听,在我们结束当前界面有用到Transition相关的动画,最好在动画结束的时候调用finishAfterTransition();而不是finish方法,这样会显得更自然一些。
哎,Transition动画在低版本不能使用,这是一件令人不太开心的事,我满怀激情的来了,你却让我洗个冷水澡,萎了咋办!!!